Graph & Equation
微分の学習において
関数 f(x) が与えられてグラフを描き，方程式 f(x)=0 を解く
という練習問題には度々出会う。ただし f(x) が3次関数など簡単な場合を除き一般に方程式は解析的には解けない。解は f(x)=0 を満たす数で数値解法による。
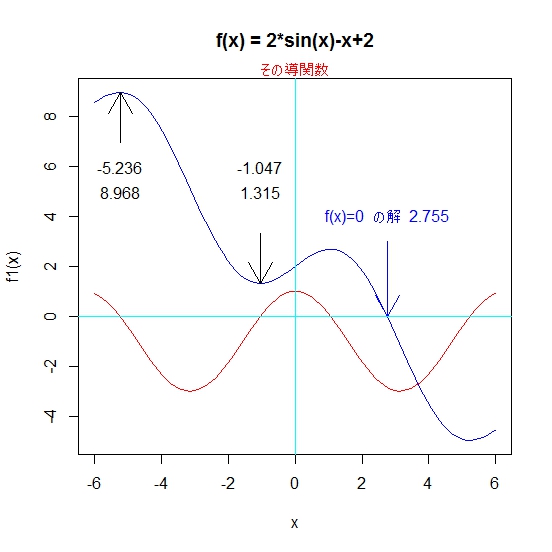
  1. f(x)=2*sin(x)-x+2のグラフを描く
    f<-function(x) 2*sin(x)-x+2 　　　で関数を定義し
    curve(f(x),-6,6)　　　でグラフを描く
  2. 方程式 f(x)=0 を解く。
    sol <- uniroot(f, c(2, 4))　　　 2≦x≦4 の範囲の解が求まる。x=2.755
  3. 極値を求める
    f1 <- deriv(~2*sin(x)-x+2, "x", func=T)　と定義
    その導関数は f2 <-function(x) attr(f1(x),"gradient")
    f1(x) f2(x)のグラフを描き unirootで f2(x)=0　の解を求め
    解はx=***＄root でそれに対する f1(x)が極値である
source