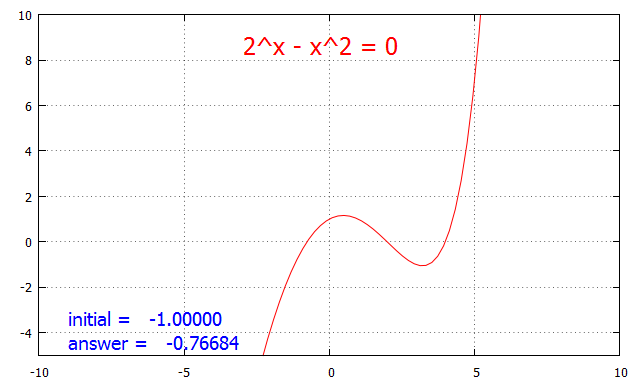
####方程式###
 f(x)=2**x-x**2
unset label
set label 5 center at screen 0.5,0.9 "2^x - x^2 = 0" 
   font "Times,18" textcolor lt 1

clear
set yrange[-5:10]
set grid;unset key
plot f(x) with lines  

####初期値###
x1=-1
set label 1 sprintf("initial = %10.5f",x1) at graph 0.02,0.12 
   font "Times,14" textcolor lt 3

####ニュートン法###
h=0.005
i=1
while(abs(f(x1))>0.00001){
 gx1=(f(x1+h)-f(x1-h))/(2*h)
 x2=x1-f(x1)/gx1
 i=i+1;x1=x2
}
set label sprintf("answer = %10.7f",x2) at graph 0.02,0.05 
   font "Times,14" textcolor lt 3
#set arrow from x2,-2  to x2,0 lw 2 lt 3
replot

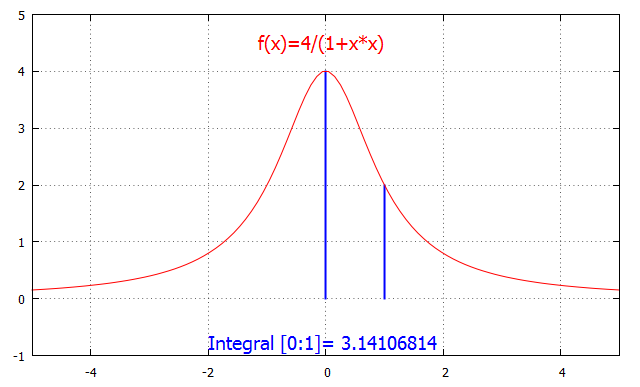
#定積分
#関数の定義とプロット
f(x)=4/(1+x*x)
set grid;unset key
set xrange[-5:5];set yrange[-2:5]
plot f(x)
#積分の上限下限ステップ
a=0;b=1
h=0.01
n=floor((b-a)/h)
s=0
#シンプソンの公式
do for [i=0:n-2] {
  xi=a+h*i   
  if (i%2==0){ s=s+f(xi)+4*f(xi+h)+f(xi+2*h)}
} 
s=s*h/3.
set label sprintf("Integral [a:b] = %10.8f",s) at graph 0.3,0.05 
   font "Times,14" textcolor lt 3
set label 5 center at screen 0.5,0.9 "f(x)=4/(1+x*x)" 
   font "Times,14" textcolor lt 1
set arrow from b,0 to b,f(b) lw 2 lt 3 nohead
set arrow from a,0 to a,f(a) lw 2 lt 3 nohead
replot
pause -1
  

 
#非線形回帰分析 
#近似する関数
f(x)=a/(1+b*x*x) 
fit f(x) "data/ex.txt" using 1:2 via a,b
plot  "data/ex.txt" using 1:2 with points,f(x) with lines
pause -1

==結果==
Final set of parameters   
　　a= 2.06521   +/- 0.05472      (2.65%)
　　b= 1.11246   +/- 0.0822       (7.389%)